4.2 円及び円弧を描く方法

4.2.1 任意の3点を通る円又は円弧を描く

（1）任意の3点A,B,Cにおいて、直線AB,BCを描き、それぞれの垂直2等分線の交点をOとする。

（2）0を中心としてOAを半径とする円又は円弧を描けば、これらはB,Cを通る。

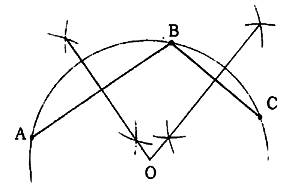
図1.16

4.2.2 等分の3点を通る円弧を描く（その1）

（1）3点A,B,Cの間にAB＝BCの関係があるものとする。ACの中点をOとすれば、OBはACの垂直2等分線である。A,CからOBに平行な直線AD,CD'（又はA,CからACの垂線AD,CＤ’）を描き、OBに等しくAE,CE'をとる。

（2）AOを任意の数に等分するが、仮に2等分することとし、その2等分点をFとする。同様AEの2等分点をGとし、FからBGに垂線を下し、その交点をHとする。同様にして、F'、G'、H'を求める。

（3）ここにH、H'は円弧ABC上の点となるので、A,H,B,H',Cをバッテンにより結べば、求める円弧が得られる。

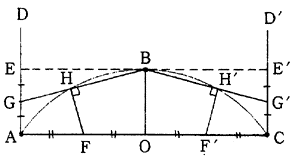
図1.17

4.2.3 等分の3点を通る円弧を描く（その2）

（1）4.2.2と同様AB＝BCの関係があるものとするA,Cを中心としてACを半径とする弧を描き、AB,CBの延長線との交点をD,D'とする。

（2）弧CDを任意の数に等分する例えば4等分するものとし、その等分点をE,F,Gとする。D点より弧上にE,F,Gと同じ等分点H,I,Jを求め、これらE〜J点とA点とを直線で結ぶ。同様にしてAD'上に同じ等分点E'〜J'点を求める。

（3）E〜Jの内側の線AEとE'〜J'の外側の線CJ'との交点をaとする同様に順次AFとCI'からAJとCE'までのそれぞれの交点をb〜fとするA,f,e,d,B,c,b,a,Cをバッテンで結べば、求める円弧となる。

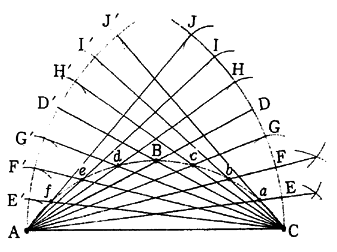
図1.18

前ページ　　　目次へ　　　次ページ